While island-hopping in the Greek Dodecanese Islands I happened to find a fascinating shop in the old town of Rhodes on the island of Rhodes. Among many other things, it sold a variety of portable sundials as well as devices for telling the time from the stars. I couldn't resist buying a portable sundial on the spot.
The two problems with a portable sundial are that it must be aligned to the north and it must be set according to your latitude. The first of these is solved by incorporating a compass, the second by using thin cord for the component which provides the shadow and putting this cord through an appropriate hole according to your latitude.
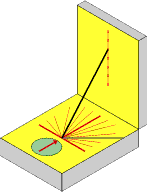
The base of the box has the usual sundial lines radiating from the point where the string is attached, marked with the hours. The lid of the box shows a list of towns in various countries across the world and indicates their approximate latitude.
The idea is that you push the cord through a hole in the lid according to your latitude, suitable holes being provided for latitudes from 36 degrees (for Rhodes) to 56 degrees (Copenhagen) in steps of two degrees. You can then move the sundial around until the compass needle points to the North position marked on the compass dial, then read off the time by noting the position of the sun's shadow made by the cord over the radial lines on the base of the box.
It isn't very accurate, of course, and it tells you the local time so you have to make an allowance for summer time, etc.. However, it is the novelty of the portable sundial which is appealing and I find the idea of this simple device quite intriguing.
The big problem is that you can't use a sundial to tell the time after the sun has set. That is where a another portable device I have comes in, which allows you to tell the time according to the angle of the two 'pointer' stars of the Great Bear.
My star clock is a small device, consisting of a couple of concentric dials and a rotatable pointer. The shop (in England) sold three models, these having dials made of brass, silver (presumably), or one of each, and the price varied accordingly. You set the pointer attached to the inner dial to point to the current month and day of the month on the outer dial, then, while holding it up to the stars with the handle at the top, you look at the pole star through a hole in the centre and rotate the pointer until it points to the two 'pointer' stars of the Great Bear. (With some, you align the pointer with Kochab in Ursa Minor.) You can then read the time from its 24-hour (inner) dial.
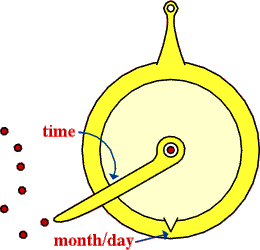
Of course, you have to compensate for daylight saving time.
Unfortunately, the one I have doesn't seem to indicate the correct time, but that is probably because I am not using it correctly. Otherwise, perhaps the markings on the dial are incorrectly positioned with respect to the pointer by about 65 degrees. It certainly seems to indicate the correct time if I set the 4.15am mark against the month/day instead of the pointer, which is against midnight.
From Spring through Autumn in Britain, it is also possible to use it by aligning the pointer with Vega, which is in Lyra, to find the time directly, but during the Winter months Vega is usually below the horizon.
I don't know whether the other examples in the shop had markings which were similarly positioned to mine. Probably not.
However, it works fine. I just have to remember to compensate by four and a quarter hours when aligning with the pointer stars of the great bear. I certainly wouldn't part with my star clock, because in my opinion the requirement that you have to compensate by four and a quarter hours significantly increases its interest, making it a collector's item!
I thought this might be possible at the time of the total eclipse in August 1999. Unfortunately, in Amiens, France, it didn't become dark enough to see the stars although we had quite a good view of the eclipse.
However, the most successful technique I developed for this purpose was to use the moon, roughly at the time of the full moon, to tell the time with the sundial. It was necessary to observe the shadow of the string using a magnifying glass. Naturally, you have to allow for the fact that the moon isn't directly opposite the Sun except at the precise time of the full moon. By making an adjustment for this, it is possible to determine the local time which can then be compared with the time found with the Star Clock.
This is the technique I use to tell the time by the stars without mechanical aids, other than a piece of string and a folded piece of paper. Alan Turing reputedly determined the time using the stars when he was cycling back to his digs from Bletchley Park late at night during the 1939/45 war, and the method I have devised is quite possibly the same method that he used.
2. For its hour hand, imagine a line from the North Star to the two pointer-stars of the Great Bear and read off the time.
3. Add four hours.
4. Subtract 2 hours for every whole month since January 1st and either subtract a further half an hour for every week into the current month or subtract four minutes for every day if you prefer, but there is no point in trying to be too accurate.
5. When appropriate, add an hour for summer time.
With luck, this technique will give you the local time accurate to within about half an hour. The tricky part is in estimating the angle of the pointer stars. A weighted length of white string is useful, as is a six-inch (15 centimetres) square of white paper with creases allowing it to be folded to provide angles of 15, 30, 45, 60 and 75 degrees. However, I doubt whether Alan Turing used either of these aids when cycling at night along the (straight) Roman Road of Watling Street.
If you intend to demonstrate this technique to a friend, a most impressive result can be obtained if you discretely glance at your watch and work backwards to determine the time you need to read from the pointer stars just before going outside!
The following is the technique in more detail.
Imagine a wide circle around the North Star which is marked out with the hour markings of a 24-hour clock, the numbers progressing anti-clockwise from the top. Thus, zero or midnight will be at the top, 6am is on the left, 12.00 midday is at the bottom, 18.00 or 6pm is on the right (and, continuing, midnight again is at the top).
midnight
.
2am. .10pm
4am. .8pm
North Star
6am. * .6pm
8am. .4pm
10am. .2pm
.
12.00 (midday)
Now find the seven stars which form the constellation known as
the Great Bear (also known as Ursa Major, or The Plough). It
looks like a saucepan, four stars forming the pan and three more
forming the arc of the handle. (Incidentally, if you continue
this ARC further around, you eventually come to a bright star
which, coincidentally, is called ARCturus.)
The 2
North Pointer
Star Stars
* * *
Great * *
Bear
*
*
* (Not to scale)
The two stars forming the side of the pan which is opposite its
handle are known as the pointer stars because they roughly point
to the North Star. (Incidentally, they straddle a point which is
30 degrees away from the North Star.)If you imagine a line from the North Star to these two pointer stars, you will have the hour hand of the 24-hour clock described above.
Example 1
During the evening of 1st January, you are likely to find the pointer stars of the Great Bear roughly to the right of the North Star. Assume the time is such that the pointer stars are in a position where you can read off the time as 6pm from the imaginary 24-hour clock scale mentioned above.
0/24 (midnight)
.
2am . .10pm
4am . .8pm
Pointer
Stars
6am. *---------*--* .6pm
Great * *
8am . Bear .
*
10am . . *
.
12.00 (midday) *
However, the time by your watch is not 6pm. To obtain the
correct time, you must follow rule number one.
Thus, 6pm plus 4 hours is 10pm. Your watch will confirm that the time is roughly 10pm.
Example 2
At the same time on 1st February, the Great Bear will be a further 30 degrees anticlockwise than it was on the 1st January (approximately). For this example, let us assume that it is a little later in the evening than above.
0/24 (midnight)
.
2am. .10pm
*
4am. * .8pm
. *
. *
.
6am. * * .6pm
Great *
8am. Bear .4pm
*
10am. .2pm
.
12.00 (midday)
When you read off the time, the line to the pointer stars might
be at about 45 degrees to the right of vertical, and you might
say, 'Ah, 9pm'. Now follow rule number one above which says,
'Add 4 hours', and you will come to 1am. Unfortunately, your
watch won't say 1am because you must additionally follow rule
number two.
Thus, 1st February is one month after 1st January so you must subtract 2 hours. 1am minus 2 hours is 11pm and your watch should confirm that the time is indeed about 11pm.
Example 3
On 1st April, and a little later at night, perhaps you will read off the time from the 24 hour clock as about 2am. Following rule number one you will add 4 hours which gives 6am. Following rule number two you will subtract 3 times 2 hours and that will bring you back to midnight. Unfortunately, your watch won't say midnight because you must follow rule number three.
If you add an hour on to midnight you will obtain 1am, and that is roughly the time your watch will be indicating.
Example 4
By the beginning of the fourth week in September, the two pointer stars will be almost directly beneath the North Star.
0/24 (midnight)
.
2am . .10pm
4am . .8pm
6am. * .6pm
.
.
8am . . .4pm
* * .
* * *
10am . .2pm
* *
12.00 (midday)
Thus, you might read off the time as midday. Add four hours and
you will come to 4pm.
I know I said above, 'the beginning of the fourth week in
September', but first let us consider 1st September. To correct
for the 1st September, subtract 8 times 2 and that brings you
back to midnight.
(i.e. 4pm = 16.00hrs. 16.00hrs - 16 = 0 = midnight)
However, because it is about three-quarters of the way through September, you need to subtract a further three-quarters of two hours, say half an hour per 8-day week. Thus, midnight minus one and a half hours brings you to 10.30pm. Conversely, you could subtract 4 minutes for every day which has passed in the current month, say 22 times 4 = 88 minutes or one and a half hours, which again brings you to about 10.30.
Finally, add an hour for summer time and you will get 11.30pm, which should roughly agree with the time shown by your watch.
There are two simple devices you can prepare which will allow you to determine the angle of the pointer stars rather more accurately than simply estimating the angle by eye.
The first is a weighted length of (white) string. This will provide a vertical.
The second is a square of paper which has been folded to have creases radiating from one corner of 15, 30, 45, 60, and 75 degrees. Using appropriate creases, this can be fashioned to provide the angle of the nearest hour, and held with one side vertical and the other side against the pointer stars.
Should you use a much more accurate device to determine the angle of the two pointer stars, rule number one can be adjusted to say that you should add roughly four and a quarter hours rather than 4 hours, and instead of subtracting 2 hours for each month you might subtract 4 minutes for each day after 1st January (subtracting 3.95 minutes per day would be marginally more accurate).
